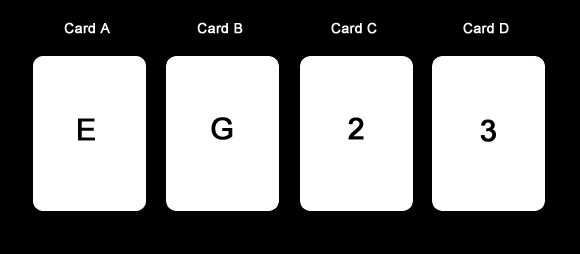
FACT: Each card has a number on one side and a letter on the other.
THESIS: Every card that has a vowel on one side has an even number on its opposite side.
REBUTTAL: Which card or cards must you turn over in order to test whether or not the Thesis is true?
Write your answer on an index card.
WHY WE CAN’T TURN ALL THE CARDS OVER.
Turning over all the cards is of course a reasonable plan, but it’s forbidden by the challenge of the puzzle, which asks “Which card or cards MUST you turn over?”
WHY WE MUST TURN OVER CARD A
The Thesis states specifically that “every card that has a vowel on one side has an even number on its opposite side.” To test that thesis, we MUST turn over card A. Anything other than an even number would refute the thesis.
WHY WE CAN IGNORE CARD B
The Thesis says nothing about consonants. Nothing on the other side of card B could prove or refute the thesis.
WHY WE CAN IGNORE CARD C
The Thesis says nothing about what’s on the other side of an even-numbered card. Yes, a vowel on one side requires an even number on the other; but an even number places no obligation on the other side. Does an even number together with a consonant refute the Thesis? No.
WHY WE MUST TURN OVER CARD D
A vowel on the other side of card D would refute the Thesis.
WHAT CARD OR CARDS MUST YOU TURN OVER?
<strong>A and D.</strong>
Only 4% of test subjects answer correctly.
WHY WE’RE FOOLED BY THE PUZZLE
—First, we’re desperate for symmetry. When someone tells us all vowel cards are even, we automatically conclude that all even cards are vowels. We’re wrong, but it happens.
—Second, we mistakenly believe that supportive examples prove a Thesis, but they don’t, at least not a Thesis that makes a categorical claim such as “Every card.” No number of supportive cards can prove such a Thesis, but a single exception can refute it.
—”Every clover has three leaves” is not proved by millions of three-leaf clovers, but it is refuted by a single four-leaf clover.
—On the other hand, the fix is easy: “Every clover has at least three leaves.”

E (Card A) and 2 (Card C).
LikeLike
Card A is the only card with a vowel. Other card might have even numbers but this doesn’t necessarily mean when flipped on the opposite side, we are guaranteed a vowel.
LikeLike
Card A and card C would have to be turned over to prove the thesis is true some card A has a vowel on it and card C has an even number on it.
LikeLike
Card A and Card C to prove the thesis is true.
LikeLike
Card A, and C because they should match if this thesis is correct matching even number to a letter with a vowel.
LikeLike
Card A and Card C. Card A has the vowel “E” meaning there is an even number on. Card C has the even number 2 on it, meaning on the opposite side there will be a vowel.
LikeLike
flip card A and card C because if there is an even number behind card A or a vowel behind card C the thesis is true.
LikeLike
Card A and Card C to see if the thesis is true flip over the car with a vowel and the card with an even number
LikeLike
card A and card C would need to be turned to prove the thesis.
LikeLike
Card A to see if a even number is on the back and card C to see if a vowel is on the back.
LikeLike
Only Card A, (Conditional Parameter)
LikeLike
E, The first card.
LikeLike
A and C
LikeLike
All of the cards could be turned over.
LikeLike
And 2, the third card
LikeLike
All of them. The thesis can be disproved if a card with a vowel has an odd number (ex if E card had a 3 on the back), it can also be disproved if G has an even number on the back(card 2), also can be disproved if 3 has a consonant on the back(card 3), or if 2 has a vowel on the back(card 4).
LikeLike
Turning over all cards can prove if the thesis is true the best choice, rather than picking one or a smaller combination of cards.
LikeLike
WHY WE CAN’T TURN ALL THE CARDS OVER.
Turning over all the cards is of course a reasonable plan, but it’s forbidden by the challenge of the puzzle, which asks “Which card or cards MUST you turn over?”
WHY WE MUST TURN OVER CARD A
The Thesis states specifically that “every card that has a vowel on one side has an even number on its opposite side.” To test that thesis, we MUST turn over card A. Anything other than an even number would refute the thesis.
WHY WE CAN IGNORE CARD B
The Thesis says nothing about consonants. Nothing on the other side of card B could prove or refute the thesis.
WHY WE CAN IGNORE CARD C
The Thesis says nothing about what’s on the other side of an even-numbered card. Yes, a vowel on one side requires an even number on the other; but an even number places no obligation on the other side. Does an even number together with a consonant refute the Thesis? No.
WHY WE MUST TURN OVER CARD D
A vowel on the other side of card D would refute the Thesis.
WHAT CARD OR CARDS MUST YOU TURN OVER?
A and D.
Only 4% of test subjects answer correctly.
WHY WE’RE FOOLED BY THE PUZZLE
—First, we’re desperate for symmetry. When someone tells us all vowel cards are even, we automatically conclude that all even cards are vowels. We’re wrong, but it happens.
—Second, we mistakenly believe that supportive examples prove a Thesis, but they don’t, at least not a Thesis that makes a categorical claim such as “Every card.” No number of supportive cards can prove such a Thesis, but a single exception can refute it.
—”Every clover has three leaves” is not proved by millions of three-leaf clovers, but it is refuted by a single four-leaf clover.
—On the other hand, the fix is easy: “Every clover has at least three leaves.”
LikeLiked by 1 person